Factorials
I’ve just started to get an interest in math and so I thought I’ll write about some of the things I’ve picked up so far. This time it’ll be about factorials, what you can use them for and how Python can help you along the way.
What it is
A factorial of a number is the product of all the numbers from one up to the number itself. For example, the factorial of 4 is 24, because
\[1 \times 2 \times 3 \times 4 = 24\]This is denoted $n!$. So, in other words, if we continue the example with 4 above, we get that
\[4! = 24\]This can be defined as general rule for all integers greater than 0 as below
\[n! = 1 \times 2 \times 3 \times ... \times n\]Lets try another example. This time we can take $5!$ as an example.
\[5! = 1 \times 2 \times 3 \times 4 \times 5 = 120\]As you can see from above, the product is growing really fast. Besides we get to do a lot of typing for bigger factorials. This is where Python comes in.
Taking help from Python
As it turns out, Python already has a function for calculating factorials. We
just need to import the math-module. The function is called factorial() so
it’s pretty straigt forward and easy to remember. So let’s give it a shot and
see how it works.
>>> from math import factorial
>>> factorial(4)
24
>>> factorial(5)
120
>>> factorial(9)
362880
Nice huh? Now we don’t have to do all the multiplication manually, we can just
start up a Python shell and import the math-module. In fact, Python is a
really nice and advanced calculator to have ready at hand. I always have a
frame in Emacs with a Python shell for doing some quick math.
What can I use factorials for then?
The most common use case I’ve read about is using it for combinatorics. For example, let’s say we have 3 different figures, a square, a circle and a cross lined up. We the help of factorials we can see that these can be placed in 6 different ways, since $3! = 6$. This can be explained as the first figure can be placed in any of the three spots that are free (because he’s first out). The second figure can be placed in any of the two remaining places. At last there is only one spot left to choose from for the last figure. And hence we get $ 3 \times 2 \times 1 = 6 $. Lets try it out visually.
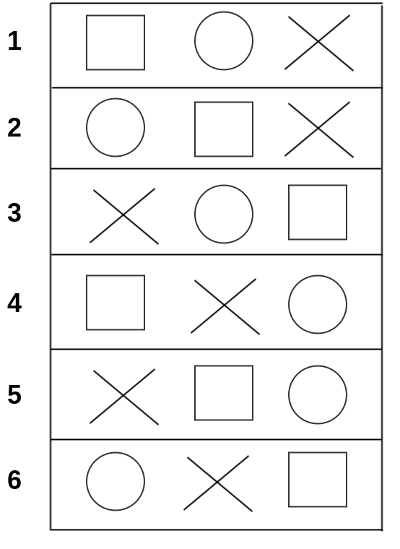
As you can see from the example above, there are no more unique possible line ups we can do. The maximum number of line ups is 6, or to put in the new way we just learned, $ 3! $. So in other words, if we have 3 figures the maximum number of unique line ups is $ 3! = 6 $. If we would have 4 figures, the maximum number of unique line ups would be $ 4! = 24 $.
